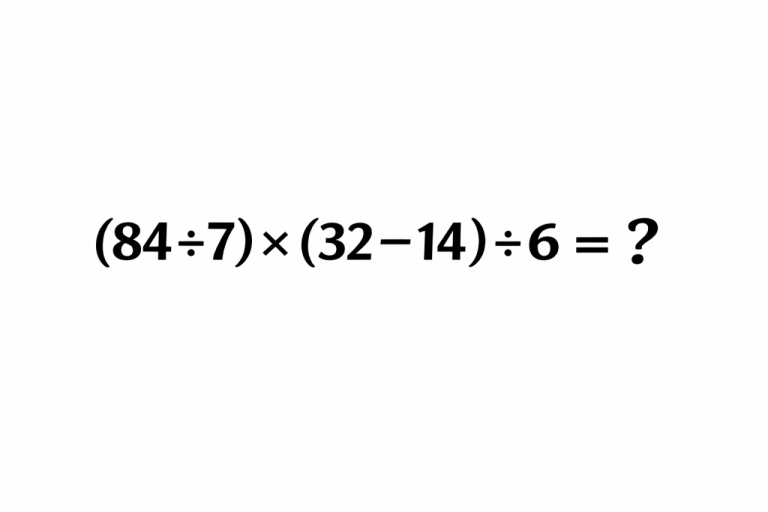Здесь нет сложных чисел, но есть ловушка в последовательности действий
Засеки 30 секунд и реши в уме, без калькулятора и без записи. В таких примерах ошибки появляются не из-за математики, а из-за привычки ускоряться там, где нужен порядок.
Почему такие задачи полезны, даже если ты давно не в школе
Мы считаем постоянно: скидки, делим суммы, прикидываем расходы, сравниваем цены, думаем, сколько осталось после пары оплат. Ошибка чаще всего рождается в голове не на цифрах, а на одном потерянном шаге. Мозг видит знакомые числа и пытается “схлопнуть” выражение быстрее, чем надо.
Короткие примеры с несколькими операциями тренируют три практичные вещи:
умение держать цепочку, спокойный темп, привычку перепроверять логику, а не первое впечатление. Это полезно в быту, потому что там нет черновика, зато есть скорость и отвлекающие факторы.
Задание
Реши в уме за 30 секунд:
(84 ÷ 7) × (32 − 14) ÷ 6 = ?
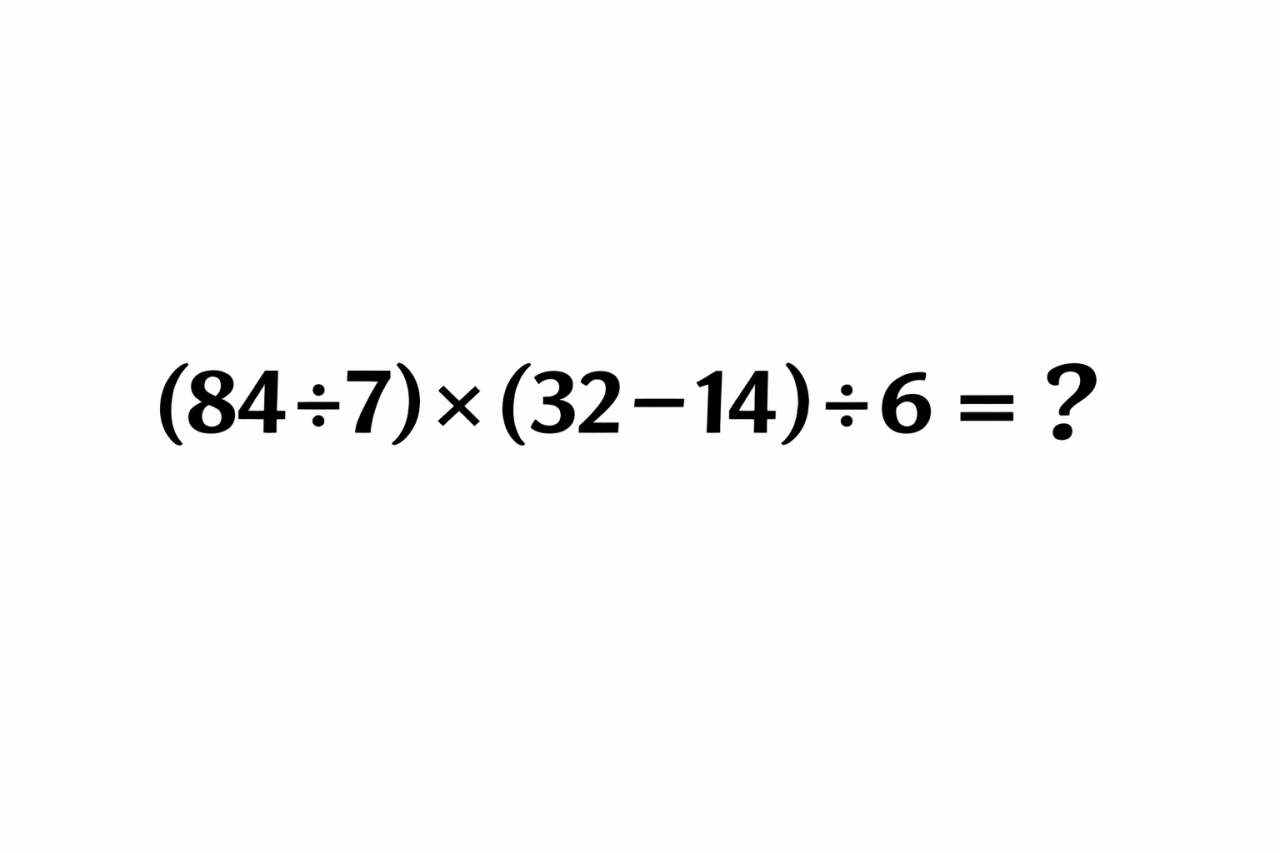
Немного интересного
Порядок действий в вычислениях появился не “для красоты”. Когда в одном выражении смешаны разные операции, правила помогают всем считать одинаково, иначе каждый получит свой ответ. Это заметили ещё в эпоху активного развития алгебры: без единого стандарта выражения читались по-разному, и споры были неизбежны. Сегодня мы воспринимаем порядок действий как само собой разумеющееся, но на практике мозг всё равно пытается упростить, особенно когда видит знакомые числа и думает, что уже понял ответ.
Ещё один любопытный момент: устный счёт хорошо тренирует рабочую память, ту самую, которая удерживает несколько шагов одновременно. Именно она чаще всего “сыпется”, когда мы спешим и параллельно отвлекаемся на сообщения, разговор или шум вокруг.
Решение
Действуем по правилам: сначала скобки, затем умножение и деление, слева направо.

Шаг 1. Деление
84 ÷ 7 = 12
Получаем:
12 × (32 − 14) ÷ 6
Шаг 2. Вычитание в скобках
32 − 14 = 18
Теперь:
12 × 18 ÷ 6
Шаг 3. Умножение
12 × 18 = 216
Получаем:
216 ÷ 6
Шаг 4. Деление
216 ÷ 6 = 36
Ответ
36
Если ты уложился в 30 секунд и не сбился, это отличный показатель: ты держишь последовательность и не отдаёшь расчёт “на автопилот”. Такие короткие задачи хороши тем, что дают быстрый тренинг внимания, без лишней теории, и со временем мозг заметно реже теряет шаг в бытовых расчётах.