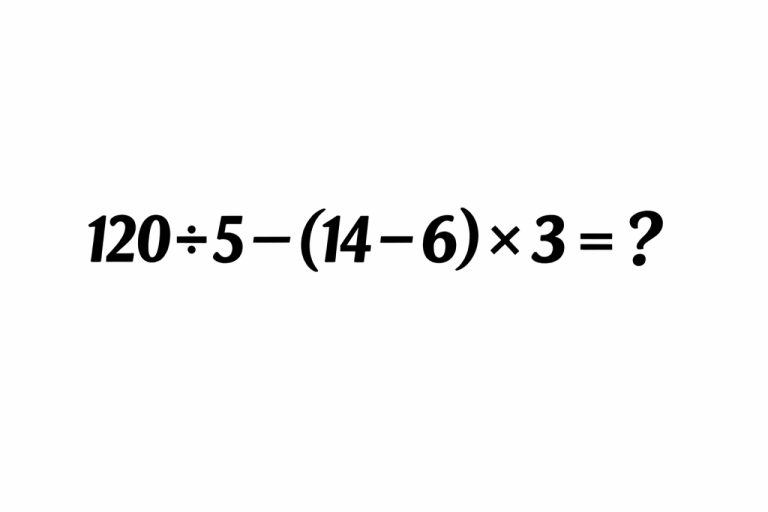Здесь нет ничего “сложного”, только скобки, деление, умножение и вычитание, но именно это и делает пример коварным
Засеки 30 секунд и попробуй решить в уме, без калькулятора и без черновика. Главная ловушка здесь не в числах, а в привычке торопиться и перескакивать шаги.
Почему такие задачи реально полезны
Мы считаем в голове постоянно, иногда даже не замечая. Цена по акции, сдача, проценты скидки, сумма нескольких мелких покупок, сколько останется после оплат. Ошибки чаще всего возникают не из-за “плохой математики”, а потому что в цепочке вычислений теряется один шаг.
Короткие примеры на порядок действий тренируют три практичные вещи:
умение держать последовательность, привычку проверять себя, спокойный темп вместо спешки. Это тот навык, который особенно выручает в быту, когда считать нужно быстро, а ошибаться не хочется.
Задание
Реши в уме за 30 секунд:
(120 ÷ 5) − (14 − 6) × 3 = ?
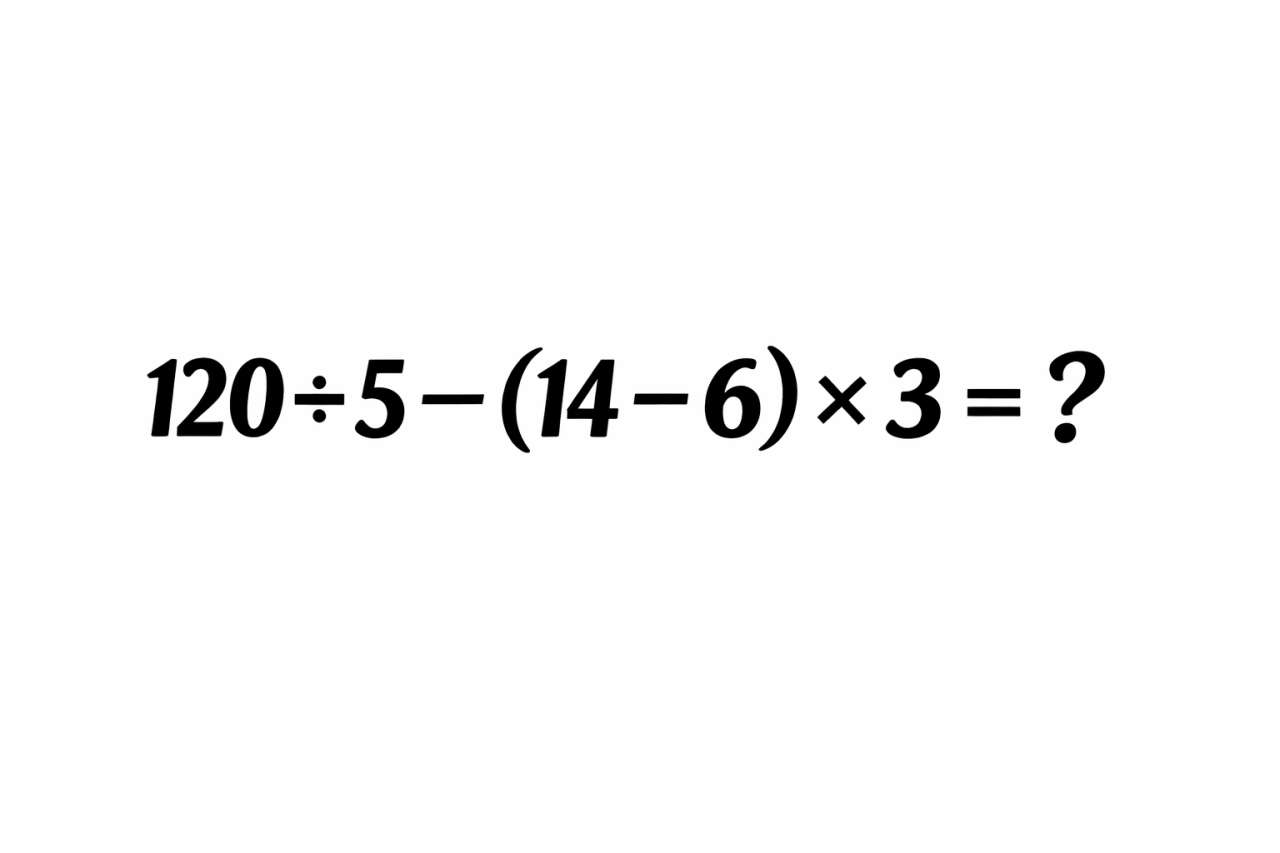
Небольшой бонус: как быстро проверять себя, не пересчитывая всё заново
Есть простой приём, который помогает поймать ошибку до того, как вы в неё поверили. После первого решения сделай “проверку здравого смысла”.
Прикинь части по отдельности. Здесь первая часть, это число около 20–30, вторая часть тоже около 20–30. Значит итог должен быть где-то рядом с нулём, не 70 и не минус 50.
Посмотри, что именно вычитается. Если обе части одинаковые, ответ будет 0. Если одна чуть больше, ответ будет маленький, положительный или отрицательный.
Привыкай держать в голове не только числа, но и смысл действия: “я вычитаю произведение”, “я вычитаю результат скобок”, это резко снижает случайные промахи.
Эта мини проверка занимает секунды, зато экономит много нервов.
Решение
Действуем спокойно и по правилам: сначала скобки, затем умножение и деление, потом сложение или вычитание.

Шаг 1. Деление
120 ÷ 5 = 24
Получаем:
24 − (14 − 6) × 3
Шаг 2. Вычитание в скобках
14 − 6 = 8
Теперь выражение такое:
24 − 8 × 3
Шаг 3. Умножение
8 × 3 = 24
Получаем:
24 − 24
Шаг 4. Вычитание
24 − 24 = 0
Ответ
0
Почему чаще всего ошибаются
Самые частые промахи здесь простые: кто-то сначала делает 24 − 8, а уже потом умножает, кто-то забывает про порядок действий и “съедает” один шаг, кто-то машинально считает 14 − 6 как 6 или 10. В таких задачах выигрывает не скорость, а аккуратность.