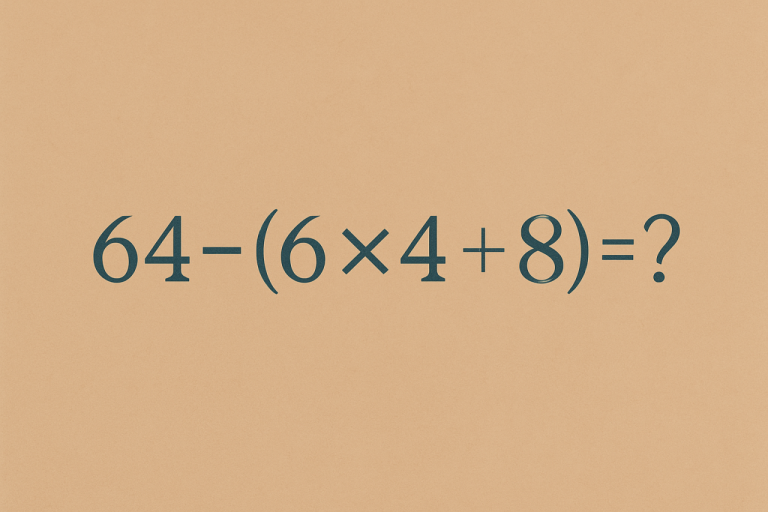Иногда, чтобы встряхнуть мозг, не нужно сложных уравнений - достаточно одного хитро составленного выражения. Именно таким и является сегодняшний тест, который проверит, насколько быстро вы умеете считать в уме и не ошибаться в скобках.
Поставьте таймер на 30 секунд, решите в уме, запишите один ответ. Ни калькулятора, ни черновика.
64 – (6 × 4 + 8) = ?
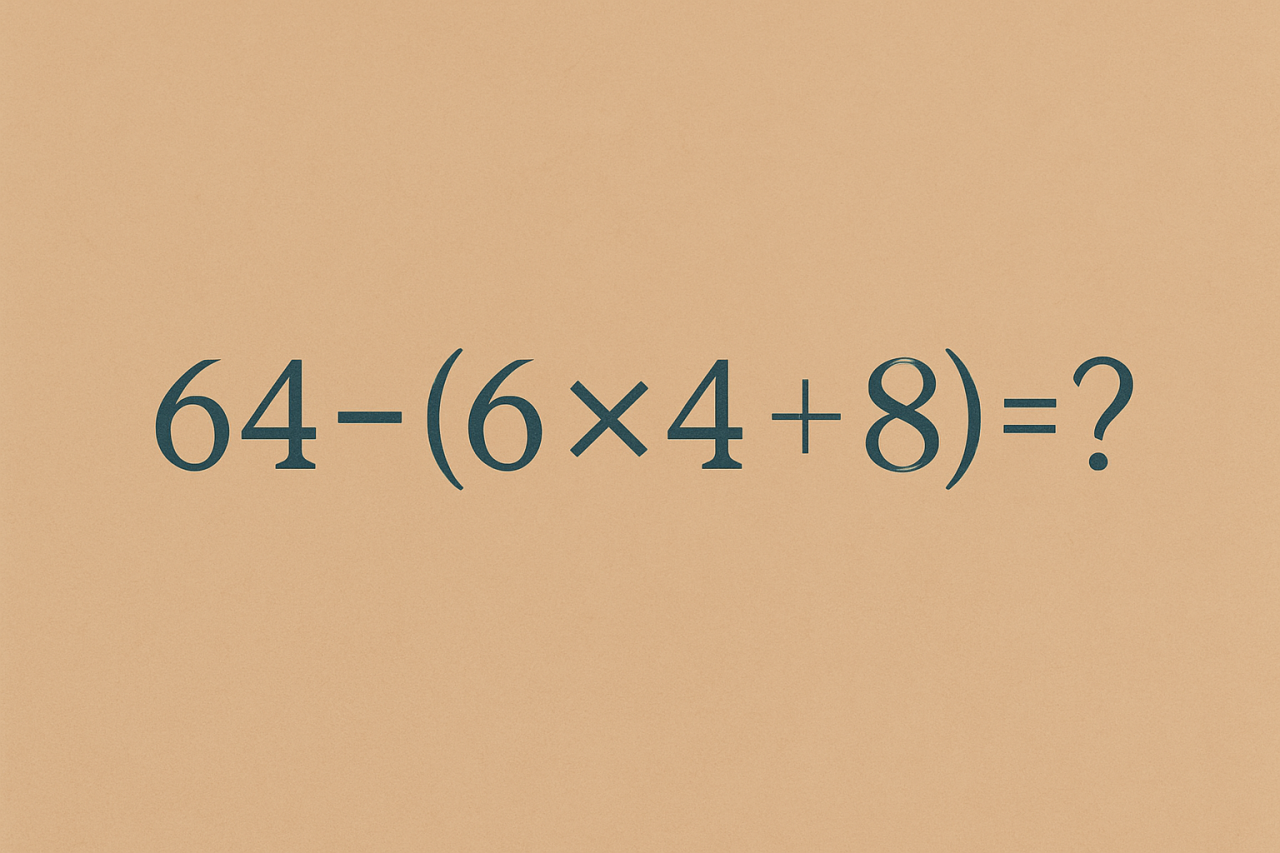
Зачем такие задачи действительно нужны
1. Прокачка когнитивного ядра
Ментальный счёт тренирует рабочую память, внимание, скорость обработки, контроль импульсов. Чтобы прийти к ответу, мозг держит промежуточные числа и порядок действий, отбрасывает лишнее, переключается между операциями. Это как спринт для лобных долей и теменной коры, где живут навыки счёта и самоконтроля.
2. Иммунитет против когнитивных ловушек
Мы часто «спотыкаемся» о видимую простоту. Скобки и приоритет действий будто очевидны, но мозг любит сокращать путь. Такие примеры учат сопротивляться иллюзии лёгкости, не поддаваться автоматизму, проверять себя, особенно в ограниченное время.
3. Эффект переноса в жизнь
- Скидки и налоги, когда вы прикидываете итоговую цену в магазине.
- Тайминг задач, когда нужно уложиться в 15 минут и распределить подпункты.
- Повседневная аналитика, от выбора тарифа до оценки процента по кредиту.
Навык быстрых расчётов делает решения точнее, а это экономит деньги и снижает стресс.
4. Мини-стресс, который укрепляет
30 секунд создают лёгкое давление, сердечный ритм чуть ускоряется, включается «тонкий фокус». Короткий вызов даёт дозированную нагрузку, мозг учится работать чётко в условиях времени, это переносится на презентации, переговоры, экзамены.
5. Микродисциплина в чистом виде
Есть правило, значит следуем ему. В математике это приоритет действий, в быту это регламент и дедлайны. Регулярная практика воспитывает привычку «сначала порядок, потом скорость», а не наоборот.
Давайте перейдем к решению. Кстати, там все не так сложно, если не волноваться:)
Решение и разбор
Шаги по порядку:
1: 6 × 4 = 24
2: 24 + 8 = 32
3: 64 − 32 = 32
Ответ: 32

Еще немного полезной информации:
История про скобки и код.
Первые языки программирования показали: машина всегда делает строго то, что вы описали. Ошибся в скобках - программа падает. Маловажной деталью скобки становятся только на бумаге, не в реальной системе. Отсюда и педагогика: учить «читать» выражение как инструкцию, а не как набор красивых символов.
Финансовая аналогия.
В формулах сложных процентов порядок операций меняет всё. Сначала применяется ставка, потом добавляются взносы, а не наоборот. Перепутайте - и итоговый капитал «потеряет» месяцы роста. Мозг, натренированный простыми примерами, не ошибётся в больших числах.
Историческая ремарка.
Правила приоритета вошли в школьную математику вместе с популярными алгебраическими учебниками XIX–XX веков. Смысл был практический: избежать неоднозначности. Стандартизированный порядок - это язык договорённости, чтобы любой расчёт читался одинаково в любой аудитории.
Такие задания учат удерживать одну цель, не распыляться, не «додумывать» за задачу. Это ровно тот навык, который спасает от многозадачности с бесконечными уведомлениями.