Математика может пугать: формулы, символы, строгие правила. Но иногда она даёт такие красивые и парадоксальные результаты, что даже самые далёкие от науки люди остаются в восхищении.
Вот 7 потрясающих открытий, которые могут изменить ваше отношение к этой науке.
1. Теорема о четырёх красках
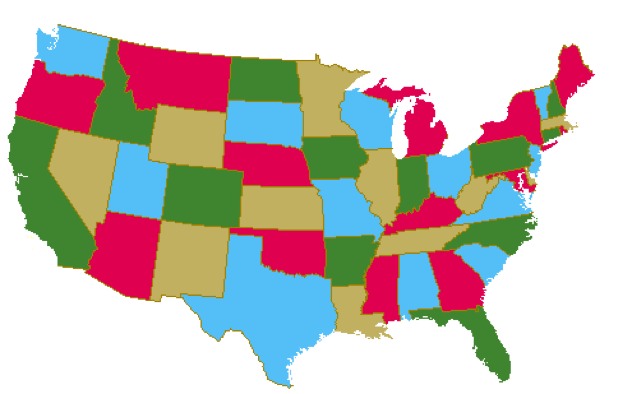
Её впервые заметил студент Франсис Гатри в 1852 году, раскрашивая карту графств Англии. Он понял, что для этого достаточно всего четырёх цветов, чтобы соседние территории не были одинаковыми. Спустя более ста лет, в 1976 году, математики доказали это с помощью… компьютера. Впервые машина помогла доказать теорему, став частью истории.
2. Парадокс Рассела

«Содержит ли себя множество всех множеств, не содержащих самих себя?» Этот логический ребус, придуманный Бертраном Расселом, привёл к революции в теории множеств. Простой на вид вопрос оказался бомбой замедленного действия для всей формальной логики XX века.
3. Последняя теорема Ферма

Ферма утверждал, что уравнение xⁿ + yⁿ = zⁿ не имеет целочисленных решений для n > 2. Он добавил: «У меня есть доказательство, но поля этой страницы слишком узки…» Загадку не могли решить почти 360 лет, пока в 1995 году Эндрю Уайлс не поставил в ней точку.
4. Формула Эйлера
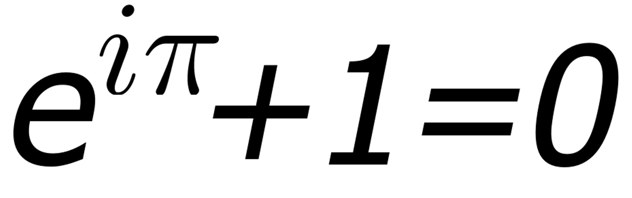
e^(iπ) + 1 = 0 - всего пять символов, но сколько смысла! Эта формула объединяет основные математические константы: e, π, i, 1 и 0. Её называют самой красивой формулой в математике, и не зря: в ней - вся гармония чисел.
5. Теорема Брауэра о неподвижной точке

Если вы берёте картинку, сжимаете, поворачиваете и кладёте обратно, всегда найдётся точка, которая останется на том же месте. Это утверждение работает даже в трёх измерениях - например, при помешивании воды в стакане. Минимум одна молекула воды всегда останется там же, где была.
6. Уровни бесконечности

Бесконечность - это не одна величина. Георг Кантор доказал: есть бесконечно много видов бесконечности. Одно дело - количество целых чисел. Другое - число всех возможных дробей. И между ними уже лежит непреодолимая пропасть.
7. Теоремы о неполноте Гёделя

В 1931 году Курт Гёдель доказал: не существует математической системы, которая могла бы доказать все истины внутри самой себя. Всегда будут утверждения, которые мы не сможем ни доказать, ни опровергнуть. Математика - это вечный поиск.